¶ Statistical analysis in SPATIAL
¶ Clustering analysis (Neighborhood-enrichment)
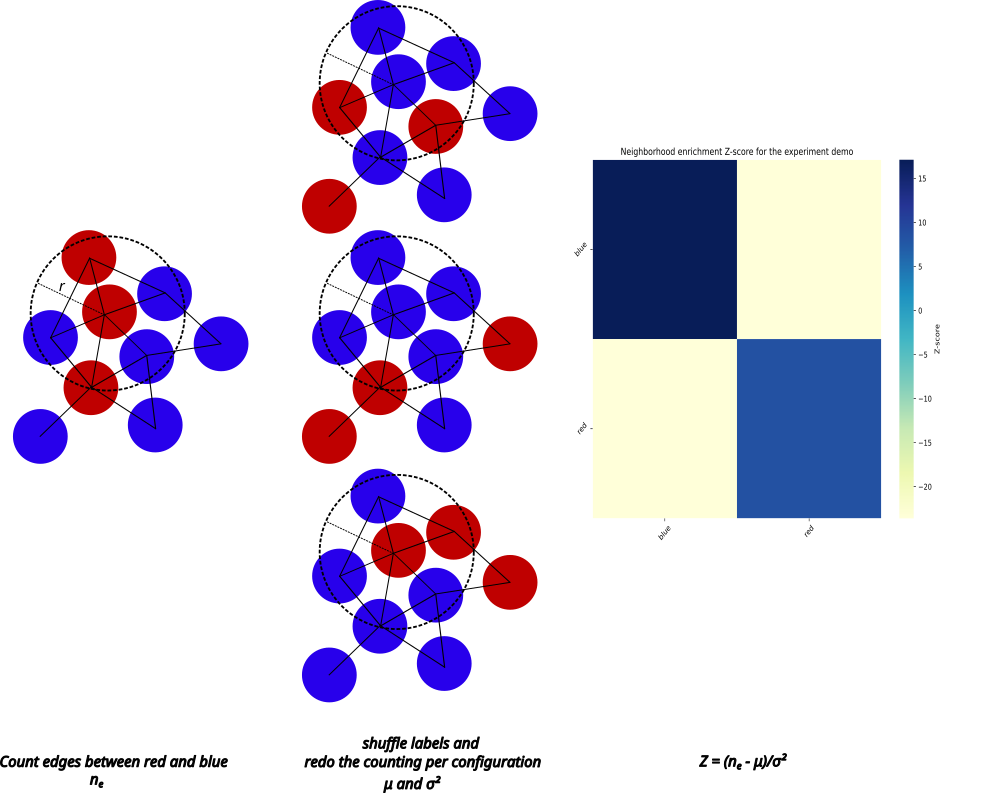
The Neighborhood enrichment score is developed to quantify the pairwise clustering of cells based on their connectivity. A positive neighborhood enrichment score means a given pair of selections are found more in each others vicinity (enriched) compared to a random distribution. We measure the enrichment as the Z-score (standard score) by comparing the number of connected cells to their completely random distribution.
To calculate the neighborhood enrichment score, we first construct a graph using the coordinates of cells from the Selection radius (r) . In this graph, each cell (node) is labeled according to the selection they belong to (any attribute visible in the "Selections" tab) and connected to other cells within the selection radius via edges. Then, for each pair of selections we count the number of connections (ne) between the connected cells. By shuffling the cell labels while keeping the connections intact, we create a large number of random configurations with the same number of cells and connections. We calculate the Z-score corresponding to the number of connections in the original configuration from the mean and standard deviation of the number of connections of the random distributions.
Further information:
Schapiro, D. et al. histoCAT: analysis of cell phenotypes and interactions in multiplex image cytometry data. Nat. Methods 14, 873–876 (2017)
¶ Tissue microenvironment analysis
¶ Recurrent spatial neighborhoods (RCNs)
Recurrent cellular neighborhoods (RCN) are proposed as groups of cells (of possibly different types) that are representative of recurring patterns of cellular organization. RCNs differ from each other in terms of their cell type composition and when taken together define the tissue from a higher level of cellular organization. An important aspect of these RCNs is that they can correspond to biologically known functional tissue areas. Identifying a correspondence between a subset of RCNs and known tissue functions can suggest relations between the other RCNs (or a collection of them thereof) and unknown or novel tissue functions.
Cell type assignment and cells’ spatial coordinates must be taken into account when computing the RCNs. Moreover, the computed RCNs should be available in all datasets, i.e. each cell from each sample should belong to only one of the computed RCNs.
If we consider each cell type a “word”, then the sample can be represented as a “document” : after all, each document is a collection of words that are ordered in a specific way. Within this line of analogy, defining RCNs from a sample can be thought of as extracting “topics” from the documents: A newspaper article can be a combination of topics “sports”, “politics”, “history”, “science” etc. Hence, once the topics are identified, they can be used to classify and group the newspaper articles. The question is, then, how can we extract these topics, without knowing anything about what “sports”, “politics”, or “science” mean?
Following the above analogy and inspired by natural language processing (NLP), we employ an unsupervised learning algorithm, called as Latent Dirichlet Allocation (LDA), to compute and extract “topics” from samples, redefine the sample as a combination of these topics which we define as cellular neighborhoods, and assign each cell to one of the cellular neighborhoods.

Further information:
Nirmal, A. J. et al. The Spatial Landscape of Progression and Immunoediting in Primary Melanoma at Single-Cell Resolution. Cancer Discov 12 (6): 1518–1541 (2022)